Calculus of variations

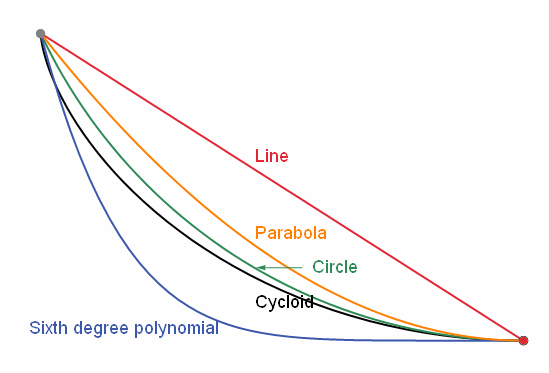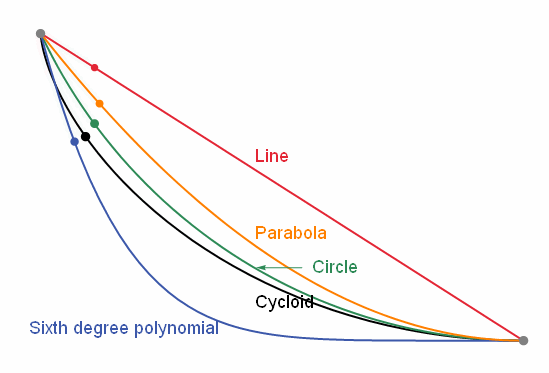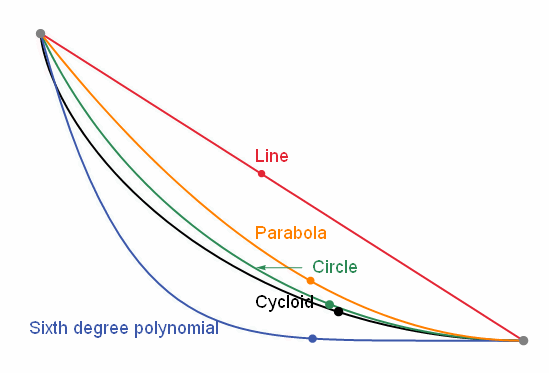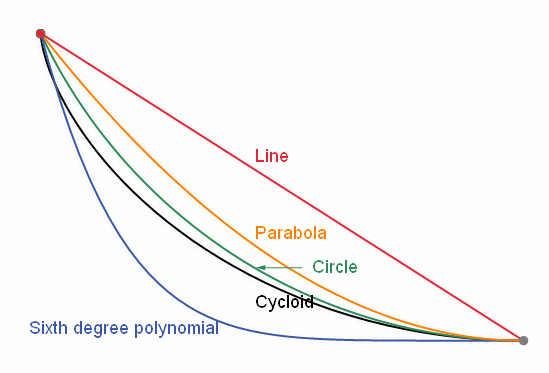
Brachistochrone problem, finding the curve that allows fastest descent without friction, a classic application. Link to wiki

A method to find extremal functions that minimize or maximize functionals, i.e. functions of a function. Given an input $x$, a function $y$ and a third function $L:{\mathbb{R}}^3\to \mathbb{R}$, functionals are typically of the form

$$J[y]=\int L(x,y(x),y^{\prime }(x))dx,$$

i.e. an integral over the function $y$ and its derivative $y^{\prime }$.

In order to do calculus, the idea of a derivative must be extended to functions, so we need to be able to take a derivative $d/dy$. This is called a functional derivative.

Euler-Lagrange equation §

The Euler-Lagrange equation gives a formula for the functions $y$ which are the extreme of $J$, similar to the first-derivative condition to see if an input minimizes or maximizes a function. This condition is necessary but not sufficient. The equation states that if $f$ is an extrema, then

$$\frac{\partial L}{\partial f}-\frac{d}{dx}\frac{\partial L}{\partial f^{\prime }}=0.$$

The calculus of variations is also related to Variational inference. There are many applications in physics, including mechanics, optics, optimal control, etc.