1996.B&A—The Robust Estimation of Multiple Motions. Parametric and Piecewise-Smooth Flow Fields (Black & Anandan, 1996)

Link to paper

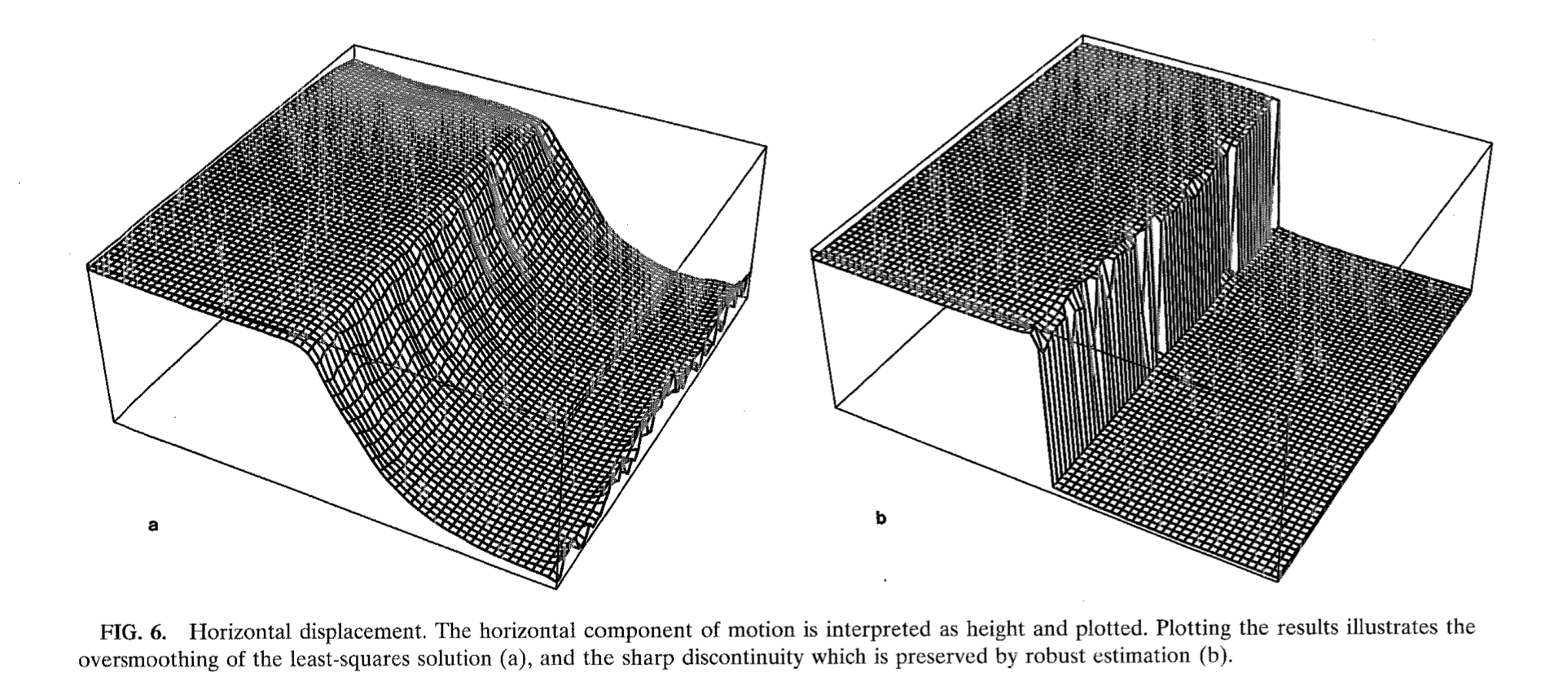
Pretty cool paper. While both typical assumptions of optical flow methods are rather well-motivated, there are important violations of both constraints that happen in the real world, both of which I’ve been thinking a lot about. There are

1. Violations of brightness constancy, which happen with “transparency, specular reflections, shadows, or fragmented occlusion (for example, looking through the branches of the tree)“. I think this is a really underappreciated point in unsupervised optical flow.
2. Violations of smoothness which happen at object boundaries, at which the optical flow is discontinuous. Currently, $L^2$ smoothness objectives create oversmoothing (as seen above).

How do we address these problems? Intuitively, it would make sense to model these explicitly and then try to reduce these. For the first, we can imagine perhaps prioritizing hue over other components (an idea I’ve been thinking about as I’ve been worrying about this), in order to reduce the penalty from shadows. For the second, we could create layered images in which the constraint is not violated within each image. However, these both suck, and they’re imperfect patches of the problem. (For each additional method of violation, you’d have to come up with another way to fix it, adding complexity to your model.)

Instead, Black & Anandan propose modifying the energy functional to be robust to outliers. As both constraints are satisfied in most of the image, we can model all exceptions, no matter their physical origin, as outliers (of different kinds). By increasing robustness to outliers, we can ideally minimize the impact of all of these simultaneously.

They use ideas from robust estimation to do this. The actual way they do this is stupid simple; they replace the $L^2$ losses within the H&S or L&K methods with truncated quadratics, or other robust functions such as these below:

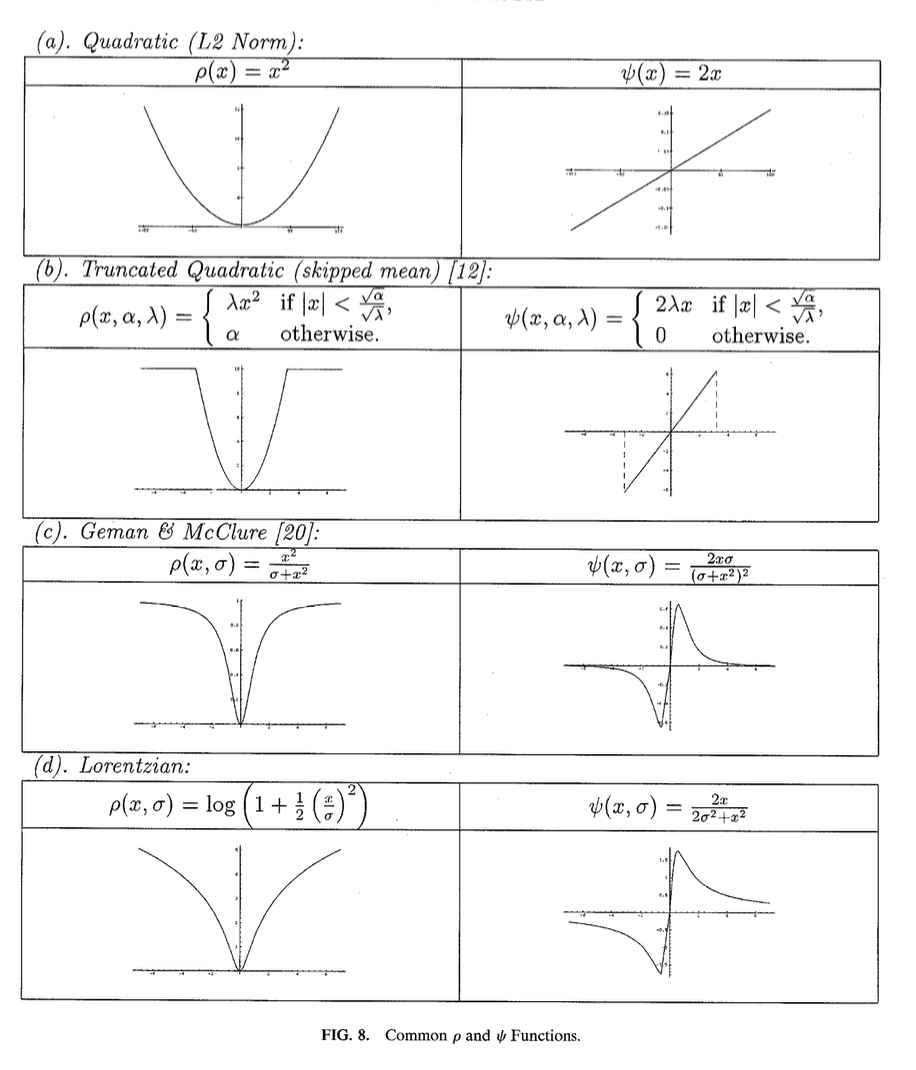
The key features of these robust estimation functions are that as $x\to \pm \infty$, ${\rho }^{\prime }(x)\to 0$. Note that the constraint is on the partial derivative of $\rho$, not $\rho$ itself (a fact which I find surprising); i.e. in plain language, at some point, increasing the error doesn’t increase the loss much further. (The right-hand $\psi$ functions are proportional to ${\rho }^{\prime }(x)$.)

I think a lot of the time they consider locally constant/affine flow functions, so L&K might be closer to what they’re doing, but their loss function looks a lot like that of H&S.

The loss objective they use is

$$E({\mathbf{u}}_s)={\rho }_D(I_x{u}_s+I_y{u}_s+I_t,{\sigma }_D)+\lambda \sum _{n\in U_s}[{\rho }_S(u_s-u_n,{\sigma }_S)+{\rho }_S(v_s-v_n,{\sigma }_S)]$$

where $\rho$ is a robust function. They demonstrate the high performance of this function in the face of discontinuities, specular reflections, fragmented occlusions, etc.

Tags §

Energy or loss minimization Robust estimation Robustness to noise Truncated quadratic objectives Multi-scale pyramids, coarse-to-fine Local methods NOT deep learning Old school Optical flow Smoothness constraints Unsupervised Affine, parameterized optical flow

Cited §

• 1989.Fwork—A Computational Framework and an Algorithm for the Measurement of Visual Motion
• 1994.BFB—Performance of Optical Flow Techniques
• 1990.F&J—Computation of Component Image Velocity from Local Phase Information (Fleet & Jepson, 1990)
• 1981.H&S—Determining Optical Flow (Horn & Schunck, 1981)
• 1981.L&K—An Iterative Image Registration Technique with an Application to Stereo Vision (Lucas & Kanade, 1981)
• 1986.N&E—An Investigation of Smoothness Constraints for the Estimation of Displacement Vector Fields from Image Sequences (Nagel & Enkelmann, 1986)

Cited By §

• 2004.BBPW—High Accuracy Optical Flow Estimation Based on a Theory for Warping (Brox… 2004)

Return: index